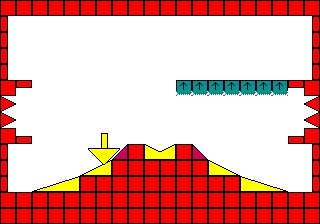
Sloped tile collisions in SGDK

• 15 June 2024
• project,
• devlog,
• sgdk,
• programming,
• witchgame,
• megadrive

Intro

I may be contacted for inqueries, complaints and insults via my bluesky account : bsky.app/profile/spacebruce.bsky.social.

The code for this article is implemented in This Github project, which has some extra goodies such as showing how to implement special tiles with varying properties.
The source code for the version described here is at the bottom of the page, if you wish to skip the explanation.

While making my funny little game for the Sega Megadrive using the SGDK framework, I struggled for a while with colliding the character and various props against a tilemap. Game engine frameworks that supply collision checking functions for the user have made me soft and weak bellied, clearly.

For my level design, I'm using Asesprite, yes, the sprite editor, which now supports working with tilemaps. Megadrive Gamedev youtuber Pigsy created a workflow for using it for SGDK projects and a script that can export an image to a C array in a text file, which I'm adopting and extending here.

You may find my personally modified version of the script with some nice-to-have tweaks here

This isn't strictly an SGDK tutorial, the fundamentals and code here can apply to any C or C++ language project, but assumptions are based around using SGDK.

Ground rules and notation

Where do collision maps come from?

A tilemap is a data structure that contains a way of figuring out what tile is at any given location in a game map.

I won't go into extreme detail describing how to create a map, but with the script supplied above you can export tilemaps from asesprite into a C array for usage as a collision map.

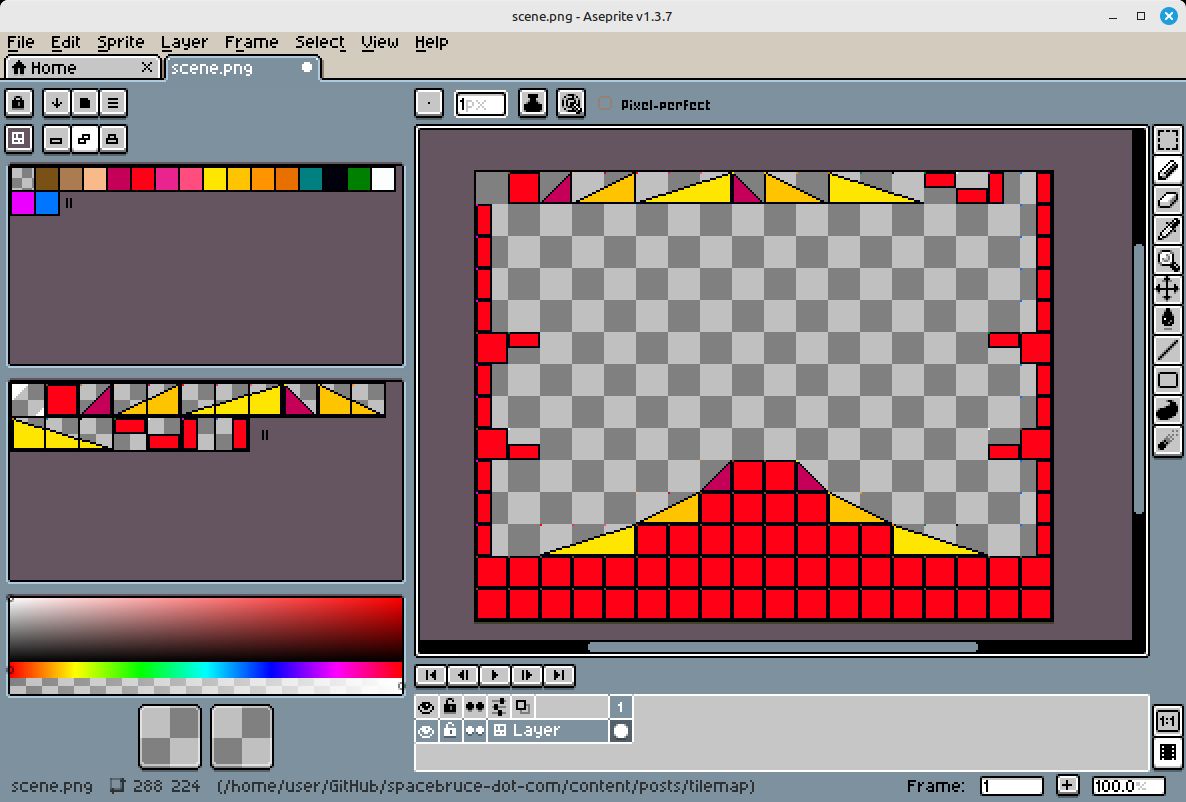
This is my asesprite setup for the map used on this page. The active layer is set to "tile" mode, which gives you the extra panel on the left. The top-left pixel of each tile corresponds to a palette index show in the panel on the left, which the script uses to figure out which tile is which when exporting the collision for game usage.
You can go over the Megadrive's palette limit of 16 here (my personal game project uses 40!), but be careful to not use those entries in graphical assets accidentally.

The purpose of running all the tiles along the top of the image in this demonstration is so Asesprite correctly recognises them as tiles in the tile plane and doesn't "erase" any you're not using, this trick helps out when debugging, but you can delete them entirely and expunge that from the map should you wish.

Once the map is built to your liking, run the script and create a new file. You can either copy that into your game project, or copy the contents in.

Tile format

I'm using this collision tileset for my game, representing all the shapes I need. My tiles are 16x16 in size and the constants used on this page reflect that.

enum TileType
{
    TileBlank = 0, 
    TileSolid = 1, TileSlopeLR = 2, TileSlopeLR2_1 = 3, TileSlopeLR2_2 = 4, TileSlopeLR3_1 = 5,
    TileSlopeLR3_2 = 6, TileSlopeLR3_3 = 7, TileSlopeRL = 8, TileSlopeRL2_1 = 9, TileSlopeRL2_2 = 10,
    TileSlopeRL3_1 = 11, TileSlopeRL3_2 = 12, TileSlopeRL3_3 = 13, TileSolidTopHalf = 14, TileSolidBottomHalf = 15,
    TileSolidLeftHalf = 16, TileSolidRightHalf = 17, 
};

You can modify these as you wish for your own usage, but ensure any change to the enum is made to the image.

Storing collision data

Here's the sample scene again containing these tiles. This PNG file is already indexed and set up correctly to import into asesprite if you'd like to monkey around with it;

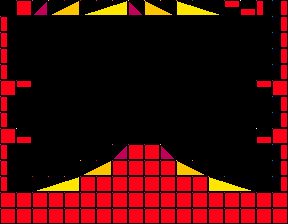
This exports to this lookup array;

static const uint8_t tilemapCollision[252] =
{
    0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17, 
    16,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,17, 
    16,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,17, 
    16,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,17, 
    16,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,17, 
    1,14, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,14, 1, 
    16,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,17, 
    16,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,17, 
    1,15, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,15, 1, 
    16,0, 0, 0, 0, 0, 0, 2, 1, 1, 8, 0, 0, 0, 0, 0, 0,17, 
    16,0, 0, 0, 0, 3, 4, 1, 1, 1, 1, 9,10, 0, 0, 0, 0,17, 
    16,0, 5, 6, 7, 1, 1, 1, 1, 1, 1, 1, 1,11,12,13, 0,17, 
    1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
    1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
};
static const uint16_t tilemapTileWidth = 288/16;
static const uint16_t tilemapTileHeight = 224/16;
static const uint16_t tilemapMapWidth = 288;
static const uint16_t tilemapMapHeight = 224;

If you squint at it, you can probably just about make out level features such as the border and mound shape in the center of the map in the numbers.

This collision engine we're using needs to keep track of the collision array and it's dimensions. For that, make a const pointer for the array and two numbers for the size. You can set them via a function like this;

const uint16_t* LevelCollisionArray;    // Pointer to a const uint16_t array, not a const pointer to a uint16_t array. 
uint16_t LevelCollisionWidth;
uint16_t LevelCollisionHeight;

void SetMapCollision(const uint16_t* CollisionArray const uint16_t Width, const uint16_t Height)
{
    LevelCollisionArray = CollisionArray;
    LevelCollisionWidth = Width >> 4;    // x >> 4 is equivalent to x / 16
    LevelCollisionHeight = Height >> 4;
}

//elsewhere
void E1M1Start()
{
    // other stuff
    SetMapCollision(E1M1Collisions, E1M1TileWidth, E1M1TileHeight);
    // more other stuff
}

Reading the tilemap back

Say you want to read a position from this point here:

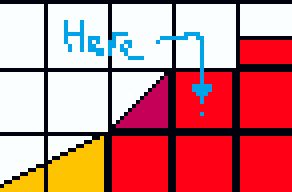
Our sample pixel is at X : 161, Y: 155. The first step to a lookup is figuring which tile the desired point lives in. Because our tiles are 16 pixels wide and tall, dividing each axis by 16 gives you the exact tile position [10, 9].

uint16_t tx = x / 16;    // Integer division rounds down
uint16_t ty = y / 16; 

Because dividing on a CPU this old is slow, you can instead calculate this with a bitshift which gives the same result:

uint16_t tx = x >> 4;    
uint16_t ty = y >> 4;

Where are we in the tile array?

The array is 1-dimensional, so we must take the tx and ty values you just created and transform them into a single index.

Here's a diagram of a 7 x 6 array, with the 2D and 1D coordinates scribbled in:

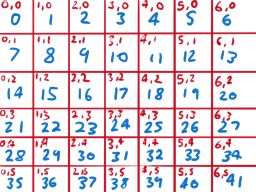
Notice how adjacent X coordinates are seperated by 1 but taking the Y up or down adds or subtracts 7, the width of the grid from the 1D index.
This can be taken advantage of, to find the 1D index from two coordinates, multiply the ty by the tile width of the map, and then add tx;

//  (ty * width) + tx
//  e.g. (3 * 7) + 2 = 23
const uint16_t tileIndex = (ty * LevelCollisionWidth) + tx;

const uint16_t tx = tileIndex % LevelCollisionWidth;
const uint16_t ty = tileIndex / LevelCollisionWidth;

Reading the array

Now the calculations to figure out the position in the map are done, you can access the array set earlier with [square brackets] like any other array in C. Here it is wrapped up in a function for ease of use:

inline uint16_t CheckMapCollisionTileFast(const int16_t& TX, const int16_t& TY)
{
    return LevelCollisionArray[TX + (TY * LevelCollisionWidth)];
}

To keep it quick, this function ASSUMES that the supplied TX and TY are within the level bounds. Go outside that and reads won't make sense and bad things may happen!

To be more practical for use, I've created here a CheckMapCollision function that transforms a X and Y pair into TX/TY values, then calls on CheckMapCollisionTileFast to do the actual work. We'll build on this function later as we add more functionality.

Here's a complete implementation for reading a slot in the array from any valid pixel postion on the map;

const int16_t TileSize = 16;
const int16_t TileCollisionShift = 4;   // 1 / 16

inline uint8_t CheckMapCollisionTileFast(const int16_t& TX, const int16_t& TY)
{
    return LevelCollisionArray[TX + (TY * LevelCollisionWidth)];
}

uint8_t CheckMapCollision(const int16_t& X, const int16_t& Y)
{
    const uint16_t tx = (X >> TileCollisionShift);
    const uint16_t ty = (Y >> TileCollisionShift);
    const uint16_t tileType = CheckMapCollisionTileFast(tx, ty);
    return tileType;
}

To call it and check the array, call on the new CheckMapCollision function

// in player code maybe!?
const bool OnGround = (CheckMapCollision(x, y) != TileBlank);

This is all you need for collision checking against solid square grid aligned blocks! If you're making a typical 8-bit style platformer game, you can close the page right now!

But if you need slopes, half blocks and more, keep reading, it gets a little trickier...

And now for shaped tiles

If you recall the tilemap image, many blocks are dedicated to different types of slopes.

We've currently only covered the empty space at the start and the block in the 2nd position.

Working with the other shapes requires a few more steps, as you not only have to figure out what tile your position corresponds to, but also where the pixel relative to that tile lookup lies.

To proceed, you have two main options;

1. Read the pixel value from the source image to determine if a pixel is occupied or not
2. Mathematically define the collision shape for every single type of tile

I'll leave the implementation of 1. up to the reader as transforming an image into a lookup is a platform dependant operation, and too slow for my needs, but in theory it should be a case of;

1. Get the pixel x and y coordinates relative to the tile
2. read the value of the source image at that location
3. return true if shaded, false if not.

You also have the hidden 3rd option of mixing and matching the two solutions depending on the type of tile if some prove trickier to implement than others.

Adjusting the collision checker

First, lets set up the framework for handling tiles. Modify the collision function to this;

uint16_t CheckMapCollision(const int16_t& X, const int16_t& Y)
{
    const uint16_t tx = (X >> 4);
    const uint16_t ty = (Y >> 4);
    const uint16_t tileType = CheckMapCollisionTileFast(tx, ty);    // The lookup function doesn't need to be modified at all

    // quick return the easy types, same as before
    switch(tileType)
    {
        case TileBlank:     // List all the "square" type tiles here, blank or not
        case TileSolid:     
            return tileType;    // Simply return whatever was detected above
        default:    
            // Nothing here, but acknowledging the default case keeps the compiler happy
        break;
    }

    // If the function is still running, calculate the tile pixel
    const uint16_t px = X % TileSize;
    const uint16_t py = Y % TileSize;

    uint16_t hit = 0;
    switch(tileType)
    {
        // slopes go here
    };

    return (hit * tileType);
};

Since we're not dealing with solid blocks anymore, we need to figure out exactly where in the block we're looking. I'm storing these tile pixels in px and py. You can get these by performing modulo 16, "wrapping" them around inside the tile-size.

In the newly extended part of the function, I'm storing a "hit" value that keeps track of if the px/py check is valid, and at the end that's multiplied by the tileType discovered by CheckMapCollisionTileFast. This helps keep the code clean and simple, so for each type of slope you simply set "hit" true or false.

Basic slopes

Lets tackle the 45" angled 1x1 slopes blocks case first.
A decending line in a block can be plotted on a graph like this, with two different points of interest marked, one above the line and one below.

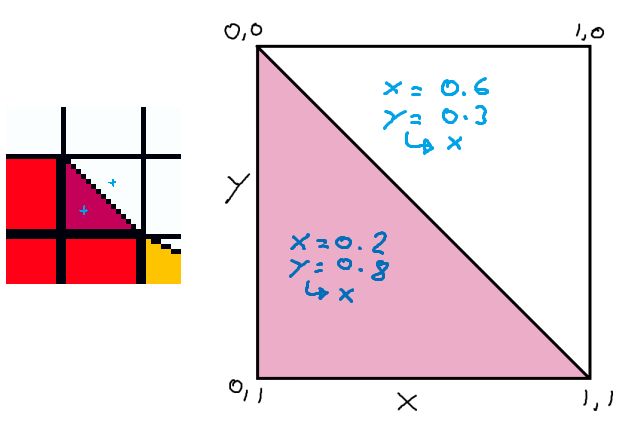
The surface line on the diagonal splits the box into two segments, the shaded half where the where the X coordinate is always greater than the Y coordinate, and one where the Y coordinate is always greater than the X coordinate.

One dot has the coordinates [0.6, 0.3], the X is larger than the Y, so it's in the top-right half. The other dot has the coordinate [0.2, 0.8], placing it in the bottom-left half.

If this seem backwards to you, remember that in a typical computer coordinate space, Y+ is Negative with 0 starting at the top of the screen/tile, which is the opposite of a normal graph.

Plugging these into the function is a case of translating those concepts to a formula and then placing them in the currently empty switch statement.

switch(tileType)
{
    case TileSlopeRL: hit = (py > px); break;  // ta da!
}

Opposite slopes

To calculate the opposite slope, where the line is ascending, flip the direction of the line. The easiest way to do that is to flip the X input! Any transformation you can apply to a graph, it's often far simpler to transform your input instead. This will be a recurring theme for the rest of this article;

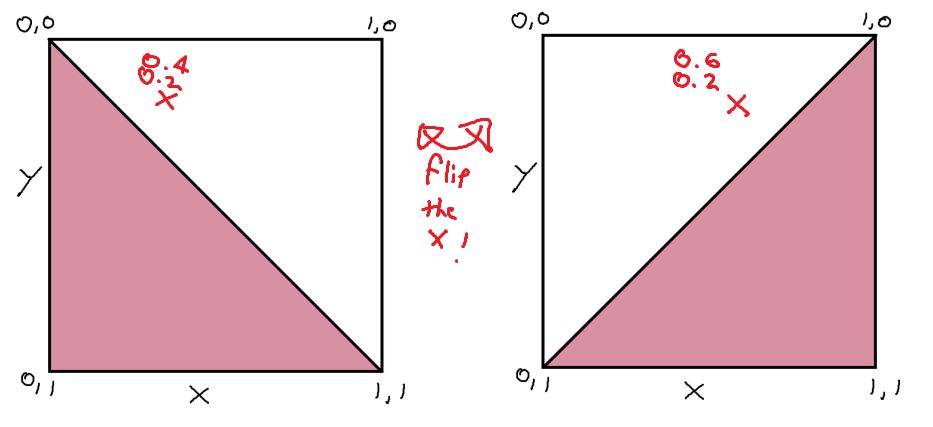
switch(tileType)
{
    case TileSlopeLR:       hit = (py > (TileSize - px));    break;
    case TileSlopeRL:       hit = (py > px); break;          break;
}

Other slopes and shapes

I'll focus on the decending slopes (x=y) for the rest of the explanations as they're simpler to describe, but for ascending shapes, subtract X from the tile width first to flip the X coordinate as above, the rest of the equation is the same. Full code for both will be at the bottom of the page.

2x1 slope

A 2x1 decending slope has the line shape y = x / 2. It's wider, but the basic question is the same. Is our Y coordinate bigger than X? The specifics of the coordinate scaling can be ignored as long as you are still asking this!

It can be drawn like this alongside a x = y 1 slope;

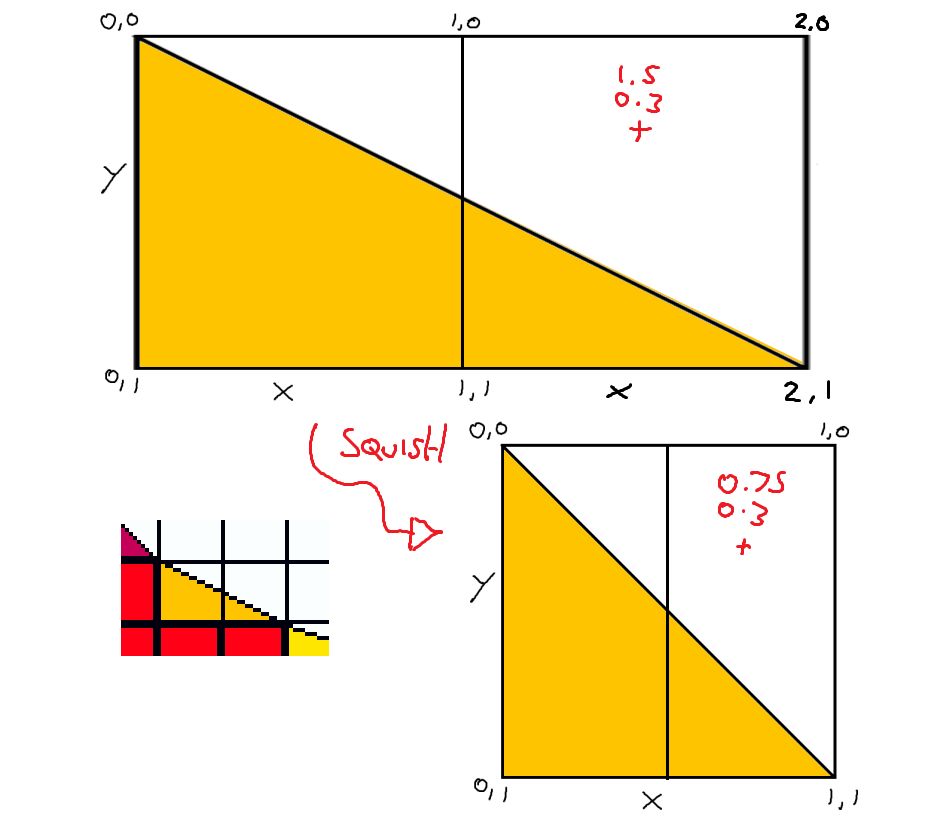
Just like y = x / 2 implies, to squeeze the shape into a 1x1 box, divide the X by 2.

To calculate the left tile of the pair, check the input X and Y inside this transformed shape;

case TileSlopeRL2_1:    hit = (py > (px / 2)); break;  // If you're skimming the page, don't do it this way!

But in 16-bit land, divide operations are slow, so looking at it from another perspective is worthwhile.

y = x / 2
x = y * 2

These both represent the same slope magnitude and thus preserve the basic question we're trying to ask! So you can switch around the code to check for y * 2 instead of x / 2 for a free speedup!

case TileSlopeRL2_1:    hit = ((py * 2) > px); break; // This is better!

The right-hand tile requires a little more brain-bending. It's a mostly empty tilewith the slope starting halfway down on the left and concluding at the very bottom-right. Continue the equation as before, adding an entire tile width to the input X to account for the half of the tile we've already covered in the first half.

case TileSlopeRL2_1:    hit = ((py * 2) > px); break; 
case TileSlopeRL2_2:    hit = ((py * 2) > (px + TileSize)); break;  

And with that you have a 2 tile wide, left-right decending slope slope, ready to go!

3x1 slope

This is mostly a repeat of the 2x1 shape, y = x / 3. The same transformations can be made on the values;

case TileSlopeRL3_1:    hit = ((3 * py) > px); break;     
case TileSlopeRL3_2:    hit = ((3 * py) > (px + (1 * TileSize)));  break;
case TileSlopeRL3_3:    hit = ((3 * py) > (px + (2 * TileSize)));  break;

You can copy and repeat this pattern for as long as you wish for different widths, 4x, 5x, the sky is the limit.

Half blocks

I've found it useful to add half-height and half-width blocks to help break up the grid pattern that make up a tile based game level, which can help make the game look less monotonous and obviously square.
For a little half height step up, check that your Y intrudes over the half-way point for a hit. Do the opposite for a block half protruding from the ceiling. For half-width blocks, apply the same logic to the X coordinate.

    case TileSolidTopHalf:      hit = (py < (TileSize / 2));     break;  //▀
    case TileSolidBottomHalf:   hit = (py > (TileSize / 2));     break;  //▄
    case TileSolidLeftHalf:     hit = (px < (TileSize / 2));     break;  //▌
    case TileSolidRightHalf:    hit = (px > (TileSize / 2));     break;  //▐

    // wouldn't do it like this personally.
    case TileSolidTopHalf:      hit = ((py * 2) < TileSize);     break;  //▀
    case TileSolidBottomHalf:   hit = ((py * 2) > TileSize);     break;  //▄
    case TileSolidLeftHalf:     hit = ((px * 2) > TileSize);     break;  //▌
    case TileSolidRightHalf:    hit = ((px * 2) < TileSize);     break;  //▐

Further extending

If you can mathematically define it, you can check against it, a wibble pattern? Look into checking against a sine wave, for example.
Very odd shaped block? Maybe use an array to define an exact shape and check px/py against that?

One last optimisation

// "inline" politely suggests to the compiler to consider inlining,  "__attribute__((always_inline))" begs 
static inline __attribute__((always_inline)) uint8_t CheckMapCollisionTileFast(const int16_t TX, const int16_t TY)
{
#if defined(__GNUC__) && defined(__m68k__)  // Use assembly version if running on Megadrive
    uint8_t result;
    asm volatile
    (
        "move.w %[LevelCollisionWidth], %%d0      \n" // Width
        "mulu.w %[TY], %%d0                      \n"  // TY * Width
        "add.w %[TX], %%d0                       \n"  // + TX
        "move.l %[LevelCollisionArray], %%a0     \n"  // LevelCollisionArray[result]
        "move.b (%%a0, %%d0.w), %[result]        \n"
        : [result] "=r" (result)                 
        : [TX] "d" (TX), [TY] "d" (TY), [LevelCollisionWidth] "m" (LevelCollisionWidth),
          [LevelCollisionArray] "m" (LevelCollisionArray) 
        : "d0", "a0"                             
    );
    return result;
#else
    return LevelCollisionArray[TX + (TY * LevelCollisionWidth)];
#endif
}

Full code

And as promised, the entire code for this article. Some of the variable names are slightly different, but the logic is the same.

No licence or strings attatched, go nuts, make something cool.

mapCollision.h

#pragma once
#include <genesis.h>

extern const uint8_t* LevelCollisionArray;   
extern uint16_t LevelCollisionWidth;
extern uint16_t LevelCollisionHeight;

enum TileType
{
    // Basic
    TileBlank = 0, 
    TileSolid = 1, 
    // Slopes
    TileSlopeLR = 2, TileSlopeLR2_1 = 3, TileSlopeLR2_2 = 4, TileSlopeLR3_1 = 5,
    TileSlopeLR3_2 = 6, TileSlopeLR3_3 = 7, TileSlopeRL = 8, TileSlopeRL2_1 = 9, TileSlopeRL2_2 = 10,
    TileSlopeRL3_1 = 11, TileSlopeRL3_2 = 12, TileSlopeRL3_3 = 13, TileSolidTopHalf = 14, TileSolidBottomHalf = 15,
    TileSolidLeftHalf = 16, TileSolidRightHalf = 17, 
};

//

void SetMapCollision(const uint8_t* CollisionArray, const uint16_t Width, const uint16_t Height);
uint8_t CheckMapCollision(const int16_t X, const int16_t Y);

// Optimised tilemap lookup
static inline __attribute__((always_inline)) uint8_t CheckMapCollisionTileFast(const int16_t TX, const int16_t TY)
{
#if defined(__GNUC__) && defined(__m68k__) 
    uint8_t result;
    asm volatile
    (
        "move.w %[LevelCollisionWidth], %%d0      \n" // Width
        "mulu.w %[TY], %%d0                      \n"  // TY * Width
        "add.w %[TX], %%d0                       \n"  // + TX
        "move.l %[LevelCollisionArray], %%a0     \n"  // LevelCollisionArray
        "move.b (%%a0, %%d0.w), %[result]        \n"  // [result]
        : [result] "=r" (result)                 
        : [TX] "d" (TX), [TY] "d" (TY), [LevelCollisionWidth] "m" (LevelCollisionWidth),
          [LevelCollisionArray] "m" (LevelCollisionArray) 
        : "d0", "a0"                             
    );
    return result;
#else
    return LevelCollisionArray[TX + (TY * LevelCollisionWidth)];
#endif
}

mapCollision.c

#include "mapCollision.h"

const int LevelTileSize = 16;

//
const uint8_t* LevelCollisionArray;
uint16_t LevelCollisionWidth;
uint16_t LevelCollisionHeight;

const uint16_t LevelLevelTileSize = 16;
const uint16_t LevelCollisionShift = 4;

void SetMapCollision(const uint8_t* CollisionArray, const uint16_t Width, const uint16_t Height)
{
    LevelCollisionArray = CollisionArray;
    LevelCollisionWidth = Width;
    LevelCollisionHeight = Height;
}

uint8_t CheckMapCollision(const int16_t X, const int16_t Y)
{
    // What tile is it in? Calls the function found in the mapCollision.h file
    const uint16_t tx = X >> LevelCollisionShift;
    const uint16_t ty = Y >> LevelCollisionShift;
    register uint16_t tiletype = CheckMapCollisionTileFast(tx, ty);

    // Decide based on what the collision found
    switch(tiletype)
    {
        case TileBlank:         // If it was ~nothing~, return TileBlank
        case TileSolid:         // If it was a solid square, return here with TileSolid.
                                // If you have any special blocks with a square profile (Say, a kill-block or trigger, consider putting defining them here)
            return tiletype;
        default:            // If it was something else, don't return here.
        break;
    }

    // What pixel in the tile is it in? 
    const uint16_t px = X % LevelTileSize;
    const uint16_t py = Y % LevelTileSize;
    
    uint8_t hit;    // Contains the result of the collision check, 0 for nothing, 1 for something
    switch(tiletype)
    {
        // Ascending slopes
        case TileSlopeLR:       hit = (py > (LevelTileSize - px));    break;                      // 1:1 slope
        case TileSlopeLR2_1:    hit = ((2 * py) > (2 * LevelTileSize - px));    break;            // 2:1 slope
        case TileSlopeLR2_2:    hit = ((2 * py) > (2 * LevelTileSize - px - LevelTileSize));   break;

        case TileSlopeLR3_1:    hit = ((3 * py) > (3 * LevelTileSize - px));    break;            // 3:1 slope
        case TileSlopeLR3_2:    hit = ((3 * py) > (3 * LevelTileSize - px - LevelTileSize)); break;
        case TileSlopeLR3_3:    hit = ((3 * py) > (3 * LevelTileSize - px - 2 * LevelTileSize)); break;

        // Descending slopes
        case TileSlopeRL:       hit = (py > px); break;                                      // 1:1 slope
        case TileSlopeRL2_1:    hit = ((2 * py) > px); break;                                // 2:1 slope
        case TileSlopeRL2_2:    hit = ((2 * py) > (px + LevelTileSize));    break;
        case TileSlopeRL3_1:    hit = ((3 * py) > px); break;                                // 3:1 slope
        case TileSlopeRL3_2:    hit = ((3 * py) > (px + LevelTileSize));  break;
        case TileSlopeRL3_3:    hit = ((3 * py) > (px + 2 * LevelTileSize));  break;

        // Half blocks
        case TileSolidTopHalf:      hit = ((2 * py) < LevelTileSize);     break;
        case TileSolidBottomHalf:   hit = ((2 * py) > LevelTileSize);     break;
        case TileSolidLeftHalf:     hit = ((px * 2) < LevelTileSize);     break;
        case TileSolidRightHalf:    hit = ((px * 2) > LevelTileSize);     break;

        // Whatever it found, it wasn't in this list, just return the value found earlier, treating the collision like a square block: 
        default:
            return tiletype;
        break;
    }

    /*
        if HIT didn't find anything, it will be 0.
        if HIT did find something, it will be 1.
        Multiply by tiletype found earlier, so if it's a slope tile (e.g. 8), the result will be 0 or 8 
    */

    return hit * tiletype;
}

Sample project

I've implemented this collision checker (And more!) into this demonstration project that you can find on my github